∆ > 0, duas raízes reais diferentes.
∆ = 0, uma raiz real.
∆ < 0, nenhuma raiz real.
Resolvendo a equação do 2º grau dentro do universo dos números reais, os casos em que
∆ < 0 não podem ser resolvidos, pois não existe raiz de número negativo dentro do conjunto dos números reais.
O surgimento dos números complexos possibilitou obter soluções para casos em que é necessário descobrir novos conjuntos numéricos, onde o quadrado de um número negativo tem como resultado um número negativo.
Iremos representar essa proposição utilizando uma unidade imaginária i, assim poderemos dizer que o quadrado de um número é um número negativo, então i * i = - 1, isto é, i² = - 1 .
Representamos um número complexo z = (x,y) sendo x Є R e y Є R, na seguinte forma: z = a + bi (forma algébrica) , onde a é a parte real de z e b a parte imaginária de z.
Exemplos:
z = 2 + 4i : Re(z) = 2 Im(z) = 4
z = 5 – 2i : Re (z) = 5 Im (z) = –2
A equação do 2º grau x² + 25 = 0 é impossível de ser resolvida no conjunto dos números Reais, mas pode ser resolvida dentro do conjunto dos números Complexos, da seguinte forma:
x² + 81 = 0 (Equação incompleta do 2º grau)
x² = –81
x = ±√–81
Temos (±9i)² = (±9)² * i² = 81 * (– 1 ) = – 81
x = ±9i
2x² - 16x + 50 = 0 (Equação completa do 2º grau)
a = 2, b = -16, c = 50
∆ = b² - 4ac
∆ = (-16)² - 4 * 2 * 50
∆ = 256 – 400
∆ = -144
Temos (±12i)² = 144i² = 144*(-1) = -144.
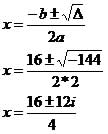
x’ = 4 + 3i e x’’ = 4 – 3i
Os números complexos são identificados por z = a + bi, onde a é a parte real e b a parte imaginária. A letra i acompanha a parte imaginária e dependo do valor de sua potência ela irá assumir um valor que irá facilitar vários cálculos.
i 0 = 1, pois todo número ou letra elevando à zero é um.
i 1 = i, pois todo número elevado a 1 é ele mesmo.
i 2 = -1, a partir dessa potência que as outras irão derivar, veja:
i 3 = i2 . i = -1 . i = - i
i 4 = i2 . i2 = -1 . (-1) = 1
i 5 = i4 . i = 1 . i = i
i 6 = i4 . i2 = 1 . (-1) = -1.
i 7 = i4 . i3 = 1 . (-i) = - i. E assim por diante.
Para descobrir, por exemplo, qual era o valor da potência i243, basta observar o seguinte: nas potências acima elas repetem-se de 4 em 4, então basta dividirmos 243 por 4, o resto será 3 então i243 será o mesmo que i3, portanto i243 = - i.
Podemos concluir que in = ir, onde r é o resto da divisão.
Forma Algébrica
Os números complexos são formados por um par ordenado (a, b) onde os valores de a estão situados no eixo x (abscissa) e os valores de b no eixo y (ordenadas). Sobre o eixo x marcamos os pontos relacionados à parte real do número complexo e sobre o eixo y os pontos relacionados à parte imaginária.
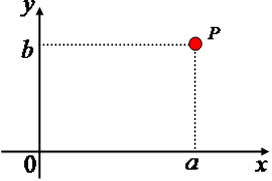
Sendo P o ponto de coordenadas (a, b), a forma algébrica pela qual representaremos um número complexo será a + bi, como a e b Є R. 
A forma algébrica de representar um número complexo é mais prática e mais utilizada nos cálculos.
Definindo as partes que formam um número complexo z = a + bi.
z é um número complexo qualquer.
a é a parte real do número complexo z.
b é a parte imaginária do número complexo z.
O conjunto dos números que formam a parte real é representado por Re (z).
O conjunto dos números que formam a parte imaginária é representado por Im (z).
Veja alguns exemplos de como identificar a parte real e a parte imaginária de um número complexo:
z = - 3 + 5i
Re(z) = -3
Im(z) = 5
z = -5 + 10i
Re(z) = -5
Im(z) = 10
z = 1/2 + (1/3)i
Re(z) = 1/2
Im(z) = 1/3
As coordenadas a e b podem assumir qualquer valor real, dependendo do valor que eles assumirem o número complexo irá receber um nome diferente:
Quando a e b forem diferentes de zero dizemos que o número complexo é imaginário:
z = 2 + 5i
Quando o valor de a é igual a zero e o de b é diferente de zero dizemos que o número complexo é imaginário puro:
z = 0 + 2i
z = 2i
Quando a diferente de zero e b igual a zero dizemos que o número complexo será real.
z = 5 – 0i
z = 5
EXERCÍCIOS
1) Resolver as equações, em C
a) x² - 12x + 40 = 0
b) x² - 8x + 116 = 0
c) x² - 6x + 109 = 0
c) x² - 6x + 109 = 0
d) x² - 4x + 68 = 0
2) Calcule
